728x90
- 회귀(Regression)이란?
- 독립변수와 종속변수 간의 상관관계를 모델링하는 통계학적 기법
- 독립변수 : 원인변수
- 종속변수 : 예측하려는 값
- 일반적으로 회귀는 예측과 분류문제에서 사용됨
- Linear Regression
- 두 변수 간의 관계를 직선으로 나타내며, 독립변수가 종속변수에 어떻게 영향을 미치는지 예측하는 통계적 기법
- 한 변수가 변할 때 다른 변수가 어떻게 변하는지 예측
- Linear Regression의 목표 : 학습데이터를 가장 잘 표현하는 직선 라인 찾는 것
- 기본 선형회귀 식
y = H(x) = Wx + b
- 'w' : Weight (가중치)
- 'b' : Bias (편향)
- 'x' : Input (입력)
- 예측 문제
- 기존 데이터를 기반으로 새로운 데이터에 대한 종속변수 값을 예측
- 독립변수 - 종속변수 간 관계식을 알고 있는 경우 독립변수만 알고 있으면 종속변수를 알 수 있음
- 매출, 부동산시세, 성적, 주식 등 다양한 분야에서 활용됨
- ex. 부동산 시세
- y = w₁x₁ + w₂x₂ + ... + wₙxₙ + b
- 독립변수와 종속변수는?
- 독립변수 : 주변시세, 역까지 거리, 학교수, 학원수, 문화 및 여가시설
- 종속변수 : 부동산시세
- 독립변수를 알면 종속변수를 알 수 있다.
- 가중치(W : Weight)
- 독립변수의 중요도를 부여하거나 단위를 바꾸기 위한 변수
- 독립변수와 종속변수 간의 관계를 정의하는 변수
- 편향(b : bias)
- 독립변수의 편향(전반적인 값)을 조절하기 위한 변수
- 비용함수(Cost Function)란?
- 모델의 성능을 측정하는 함수
- 모델의 예측 값과 실제 값의 차이를 측정 (그 차이를 비용이라고 함)
- 컴퓨터가 무엇인가 예측했을 때 얼마나 틀렸는지를 알려줄 수 있다.
- 일반적으로 평균제곱오차 (Mean Squared Error, MSE) 함수를 사용하여 비용을 측정한다.

- 선형회귀 예제 : 학습시간에 따른 점수 예측
- 모델이 다음과 같이 정의되었을 때 비용과 평균비용을 구하자.
- H = Wx + b, w=3, b=35
- 모델이 다음과 같이 정의되었을 때 비용과 평균비용을 구하자.


- 최적화(Optimization)
- 목적을 달성하기 위한 최적의 파라미터를 찾는 과정
- 목적 : 독립변수와 종속변수 사이의 관계를 잘 설명하는 모델을 만드는 것
- 목표 : 비용을 최소화로 한다.
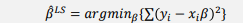
- 해야 할 일 : 비용을 최소화 하는 w와 b를 찾는 것
- 어떤 알고리즘을 통해 모델이 데이터로부터 스스로 최적의 값을 찾아 나가는 과정을 학습(Training)이라고 한다.
- 선형회귀 모델의 최적화
- 선형회귀 모델의 최적화 과정을 이해하기 위해서는 선형회귀 모델의 W와 B에 따른 비용특성을 알아야 한다.
ex. b는 0이라고 가정, W의 값을 [-5, 2, +10]으로 값을 바꿔가면서 비용 계산

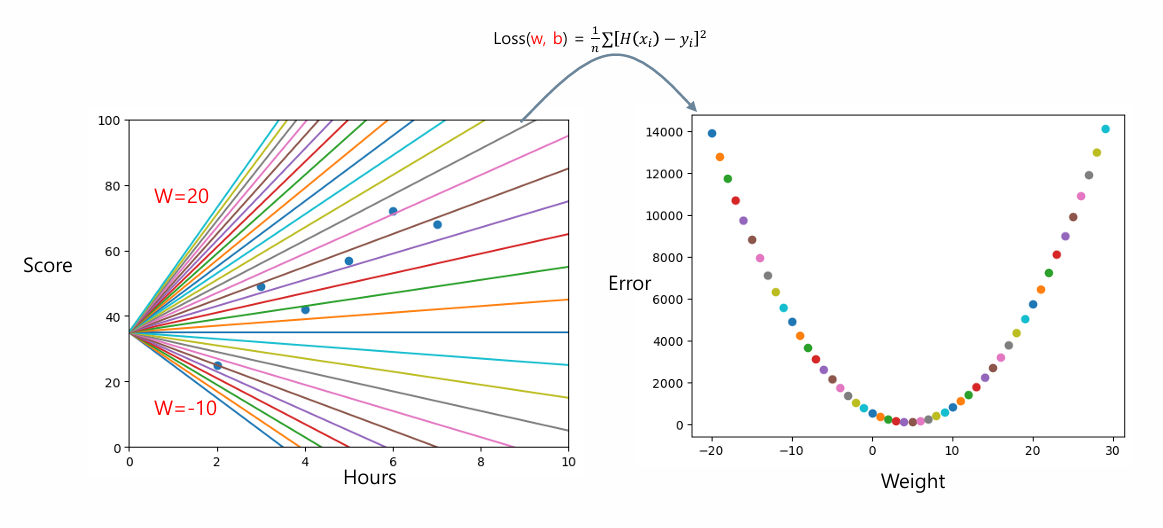
- 경사하강법(Gradient Descent)
- 함수의 기울기를 이용하여 함수의 최소값을 찾는 방법
- 함수의 기울기는 편미분을 통해 구한다.
- 기울기의 특성
- 최적의 w값이 무엇인지 모르지만 앞 예제를 통해 비용을 최소로 하는 최적의 값이 존재한다는 것 확인
- 최적의 값 보다 작은 수에서 조금식 큰 수를 대입해보면 비용이 작아지는 경향
- 최적의 값 보다 큰 수에서 조금씩 작은 수를 대입해보면 비용이 작아지는 경향

- 기울기의 방향
- 최적값은 기울기가 0이 되는 지점
- 기울기가 0이 되는 지점을 기준으로 왼쪽에서는 항상 음수 값을 가지며 오른쪽에서는 항상 양수 값을 가짐

- 경사하강법
- 정의


- 학습률 : a
- 학습률이란 경사하강법의 이동거리를 조절하는 값

- Overfitting 과 Underfitting
- Overfitting
- 과대적합으로 학습용 데이터에 과하게 학습되어 실제 테스트데이터에 대해 성능이 현저하게 떨어지는 경우
- Underfitting
- 과소적합으로 학습용 데이터에서 학습이 제대로 안되어 성능이 떨어지는 경우

- regularization (정규화)
- 모델 학습 시 손실함수(Loss function)에 패널티 항(a penalty term)을 추가하여 모델이 과대적합되지 않도록 함

- 학습 기반 모델의 특징 : Error VS 모델 복잡도
- 모델의 복잡도가 매우 작을 때 : Underfitting 상태 - 낮은 성능, 학습/테스티 시 모두 큰 오류를 보여줌
- 모델의 복잡도가 매우 클 때 : Overfitting 상태 - 높은 학습 성능, 낮은 테스트 성능 보여줌
- 모델의 복잡도가 적정일 때 : 학습/테스트 시 모두 좋은 성능 보여줌

- 좋은 모델을 만드는 방법
- 일반적으로 학습데이터에 좋은 복잡한 모델을 만들고 모델을 단순화 시키는 과정을 거치면서 튜닝
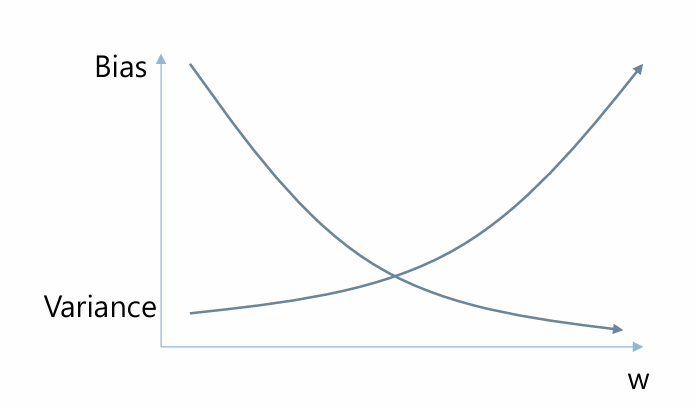
- 모델의 Parameter (W) 에 따른 손실함수 특성 분석
- W값이 클수록 Low bias, High variance => Overfitting 가능성
- W값이 작을 수록 High bias, Low variance => Underfitting 가능성
- Regularization : Lasso and Ridge
- Lasso regularization
- 일부 가중치를 정확히 0으로 설정하여 모델의 복잡도를 줄이는 효과
- 고차원 데이터에서 중요하지 않은 특성을 제거하여 해석이 가능한 모델을 제공
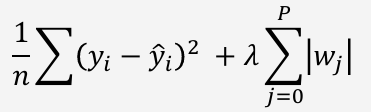
- Ridge regularization
- 모든 가중치를 작게 만들지만 0으로는 설정 X
- 상관관계가 높은 변수들을 적절히 조정하여 모델 안정성을 높임

| 특징 | Lasso | Ridge |
| 패널티 형태 |  |
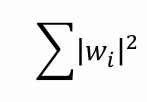 |
| 변수 선택 | 일부 가중치를 0으로 만들어 변수 선택 가능 | 모든 가중치가 축소되지만 0으로 만들지 않음 |
| 모델 형태 | 희소 모델 | 모든 변수 포함 모델 |
| 적용 데이터 | 특성이 많지 않은 경우 효과적 | 상관관계가 높은 변수들이 많은 경우 효과적 |
- Outlier
- 이상치란 다른 관측값들과 크게 다르거나 극단적으로 벗어난 값을 의미
- 원인?
- 데이터의 입력 오류 , 시스템 오류 , 특이한 값
- 해결방안 => RANSAC
- RANSAC
- Random Sample Consensus의 약자, 데이터에서 이상치의 영향을 최소화하면서 모델을 학습하기 위한 알고리즘
- 동작 방식
- 모델 초기화 - 전체 데티어테서 임의의 데이터를 선택하여 초기 모델 생성
- 모델 평가 - 생성된 모델을 기반으로 허용오차(Threshold) 범위에 있는 내부치(Inlier)를 찾음
- 최적화 - 1,2번 과정 반복 / 내부치의 개수가 많으면 최종 추정 모델 갱신 / 일정 횟수 반복 후 종료하거나 Inlier의 비율이 일정 수준 이상일 경우 조기 종료
- RANSAC 최적화
- 최적의 모델 모습?
- 내부치만을 포함하는 샘플을 선택하여 모델을 학습할 때 최적의 모델이 나올 수 있음

- RANSAC의 장단점
| 구분 | 내용 |
| 장점 | - 이상치에 강건, 다양한 모델에 적용 가능 - 구현이 간단하며 노이즈 데이터 처리에 강함 |
| 단점 | - 반복 횟수 증가로 인한 시간 비용 증가 - 매개변수 설정에 민감 - 결과의 불안정성 |
| 적합한 경우 | - 이상치가 많은 데이터 - 노이즈가 많은 경우 - 정확한 모델 학습이 중요한 경우 |
| 적합하지 않은 경우 | - 내부치 비율 추정이 어려운 경우 - 대규모 데이터 - 다중 모델 문제 |
728x90
'인공지능' 카테고리의 다른 글
| 인공지능(7) - K-Means Clustering (0) | 2025.03.10 |
|---|---|
| 인공지능(6) - K-Nearest Neighbor (0) | 2025.03.10 |
| 인공지능(5) - HMM : Hidden Markov Model (0) | 2025.02.12 |
| 인공지능(4) - Minimax (0) | 2025.02.11 |
| 인공지능(3) - Fuzzy Logic (0) | 2025.02.10 |
