728x90
- Sequential Data
- 특정 순서를 가지는 데이터 (EX. 쇼핑몰 구매 목록, 영화 시청 목록)
B가 발생할 확률?
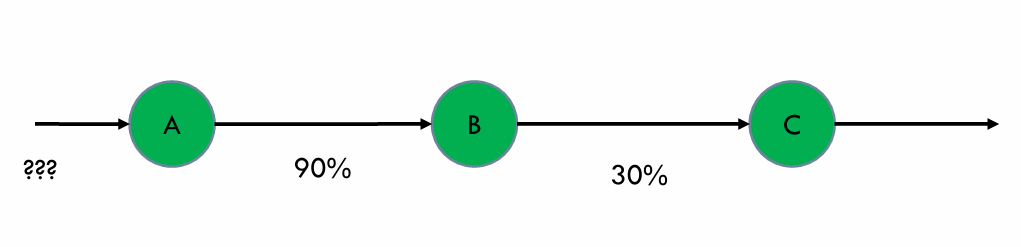
- Forecasting Problem
- N discrete states 중 하나의 상태를 갖는 시스템을 고려
- 정의된 상태는 랜덤으로 변하는 stochastic systems이라고 가정
- 이때 joint distribution은 거의 계산 불가능
- p(q₀, q₁, ... qₜ) = P(q₀)P(q₁|q₀)P(q₂|q₁q₀)P(q₃|q₂q₁q₀)...

특정 상태의 확률 값은 이전 상태의 확률 값을 알면 구할 수 있다.
- 과거의 모든 상태를 구하는 것은 거의 불가능 하다.


- Markov Property
- Markovian property
- 다음 미래의 상태는 오직 현재 상태에 영향만 받는다(가정)
- P(qₜ₊₁ | qₜ , ... , q₀) = P(qₜ₊₁ | qₜ)
- 현재 상태가 주어지고 이전 과거의 상태는 고려하지 않는다.
- 바로 직전의 정보가 충분히 과거의 정보를 담고 있다고 가정한다.
- 현재 상태가 미래를 예측하는데 충분한 정보를 담고 있다고 가정한다.
- 다음 미래의 상태는 오직 현재 상태에 영향만 받는다(가정)
- Markov Process
- Markov process 는 랜덤 프로세스이다.
- 확률적인 행동(Stochastic behavior)을 표현하며, 연속적인 행동의 변화를 관찰한다.

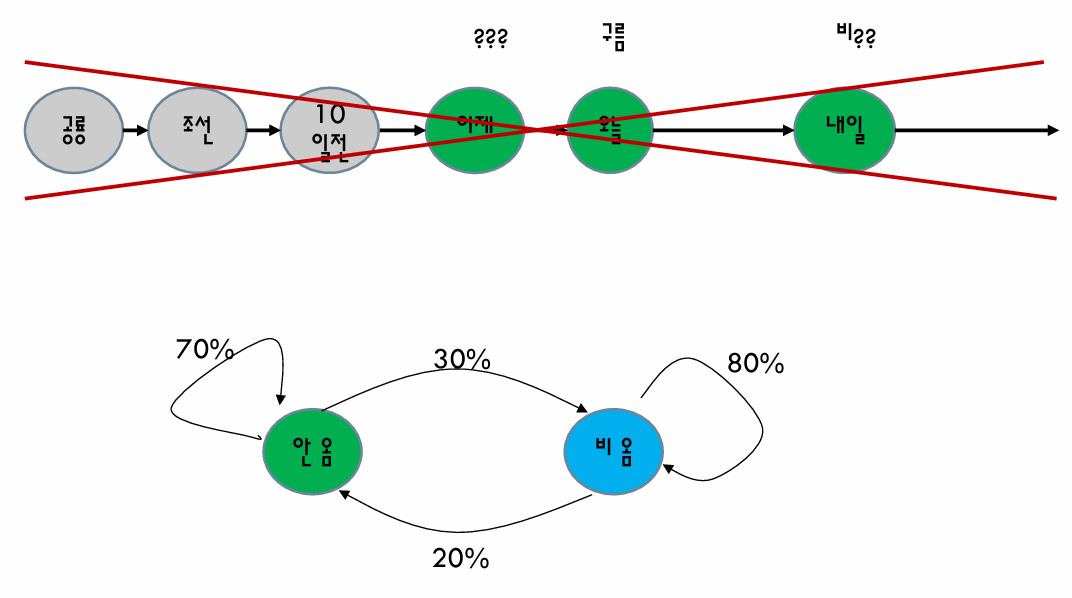
- State Transition Matrix
- Markov state s와 성공 상태 s'에 대해, 상태 변화 확률은 다음과 같이 정의
- Pₛₛᶥ = P(Sₜ₊₁ = s' | Sₜ = s)
- 상태변화 행렬 P는 모든 상태s로부터 다음 상태 s'로 변할 확률을 정의

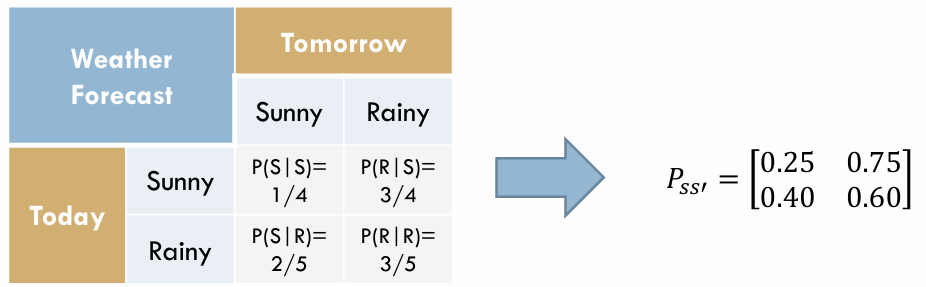
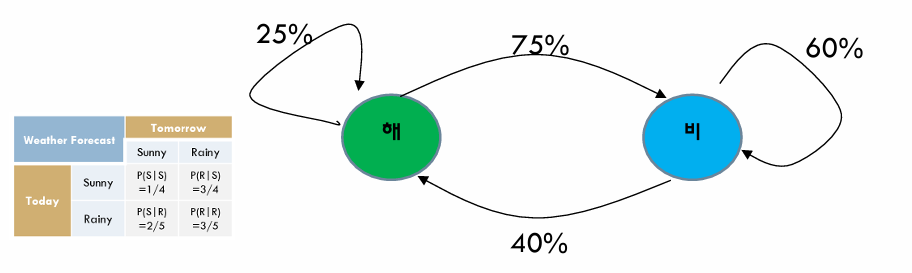
- Example : MP
- MP를 이용하여 날씨를 예측하는 모델을 만들고자 함
- 모델을 만들기 위해 다음과 같이 10일 동안 날씨를 관찰하여 데이터를 수집하였다. 이를 기반으로 Markov Process 모델을 완성하고 7월 12일의 날씨를 예측

- 상태 : 해 / 비
- 상태 전이 확률 : P(S|S), P(R|S) , P(S|R), P(R|R)

- P(S|S) = ¼ , P(R|S) = ¾ , P(S|R) = ⅖ , P(R|R) = ⅗ 이 나온다. (여기서 7/10은 다음날을 구할 수 없으므로 확률에서 제외한다.)
- 상태 전이 확률 행렬 (State transition matrix)
- 모델
- 날씨 예측

- 문제점
- 확률이 높은 state로 수렴
- 해결방법 : 데이터를 관측하여 확률 값 업데이트
- Hidden Markov Model 이란?
- 같은 시간에 발생한 두 종류의 state sequence 각각의 특성과 그들의 관계를 모델링
- Type 1 state sequence : (s₁,s₂, ..., sₜ)
- Type 2 state sequence : (s₁',s₂', ..., sₜ')
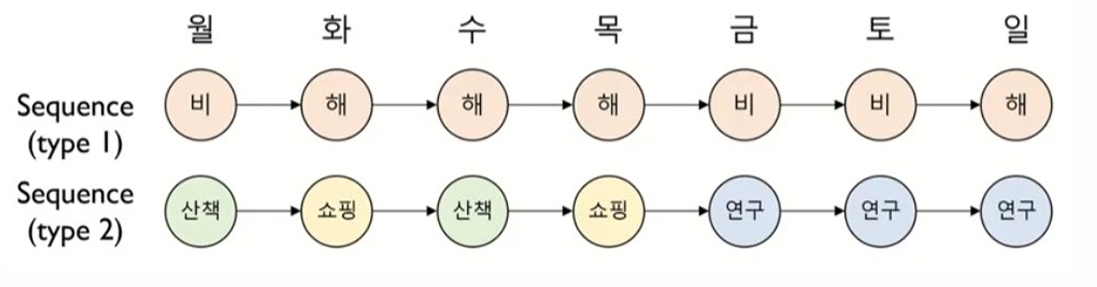
- Type 1 sequence는 숨겨져 있고(Hidden), Type 2 sequence는 관측이 가능(Observable)
- Hidden sequence 가 Markov assumption을 따름 -> 순차적 틍성을 반영
- Observable sequence 는 순차적 특정을 반영하는 Hidden state에 종속
- Hidden Markov Model (HMM) 예제 (Observable vs Hidden)
- 특정인의 행동 (쇼핑, 연구, 산책)에 따라 날씨 추측
- 빈대떡 소비량에 따른 날씨 추측
- 중국음식 배달량에 따른 날씨 추측
- 공 색깔 정보에 따라 그 공이 담겨있는 상자의 종류 추측
- HMM : Parameters
- Parameters of a Hidden Markov Model
- A(aᵢⱼ) : 상태전이확률 행렬(State transition probability matrix)
- B(bⱼₖ) : 방출확률 행렬(Emission probability matrix)

- π(πᵢ) : 초기 확률(Initial state probability matrix)

- Parameters of a Hidden Markov Model : λ = {A,B,π}
- 상태 전이 확률 A = |aᵢⱼ|
- A -> HMM이 작동하는 도중 다음 상태를 결정
- 방출 확률 B = |bⱼ(vₖ)|
- B는 HMM이 어느 상태에 도달했을 때, 그 상태에서 관측될 확률 결정
- bⱼ(vₖ) : 은닉상태 bⱼ에서 관측치가 vₖ가 도출될 확률
- 초기 상태 확률 π = (πᵢ)
- π -> HMM을 가동 시킬 때 어느 상태에서 시작할 지 결정
- πᵢ -> sᵢ 에서 시작할 확률
- 상태 전이 확률 A = |aᵢⱼ|
- HMM의 세 가지 문제
- Evaluation problem : HMM(λ*)과 O가 주어졌을 때 Observable sequence O'의 확률
- Decoding problem : HMM(λ*)과 O가 주어졌을 때 hidden state sequence를 찾는 문제
- Learning problem
- Evaluation problem
- Foward algorithm
- 오늘 산책, 내일 산책, 모레 연구, 글피 쇼핑할 확률은?

O = (o1=산책, o2=산책, o3=연구, o4=쇼핑)
Probability(O) = P(O) = P (o1=산책, o2=산책, o3=연구, o4=쇼핑) = ???
- Forward Probability (전방 확률, aₜ(i))

- a₁(1) = π₁⋅b₁(산책) = 0.6 ⋅ 0.1 = 0.06
- a₁(2) = π₂⋅b₂(산책) = 0.4 ⋅0.6 = 0.24
- a₂(1) = (a₁(1) ⋅ a₁₁ + a₁(2) ⋅ a₂₁) ⋅ b₁(산책) = (0.06 ⋅ 0.7 + 0.24 ⋅ 0.4) ⋅ 0.1 = 0.0138
- a₂(2) = (a₁(1) ⋅ a₁₂ + a₁(2) ⋅ a₂₂) ⋅ b₂(산책) = (0.06 ⋅ 0.3 + 0.24 ⋅ 0.6) ⋅ 0.6 = 0.0972
계속 구하다 보면

- Forward probability는 주어진 Sequence O가 HMM에 속할 확률 문제에 활용 가능하다.
Forward Probability 앞으로(시간 순으로) 확률 계산 <-> Backward Probability 뒤로(시간 역순으로) 확률 계산
- Decoding problem (HMM의 핵심)
- Problem : HMM(λ*)과 O가 주어졌을 때 최적의 S결정(가장 그럴싸한 은닉상태 시퀀스 결정)
- Solution : Viterbi Algorithm
- 오늘 산책, 내일 산책, 모레 연구, 글피 쇼핑을 했다면 각 날들 날씨는?


- v₁(1) = π₁⋅b₁(산책) = 0.6 ⋅ 0.1 = 0.06
- v₂(2) = π₂⋅b₂(산책) = 0.4 ⋅ 0.6 = 0.24
Viterbi 확률 vₜ(i) : t번째 시점의 i은닉상태 확률
- v₂(1) = max(v₁(1) ⋅ a₁₁, v₁(2) ⋅ a₂₁) ⋅ b₁(산책) = max(0.042, 0.096) ⋅ 0.1 = 0.0096
- v₂(2) = max(v₁(1) ⋅ a₁₂, v₁(2) ⋅ a₂₂) ⋅ b₂(산책) = max(0.018, 0.144) ⋅ 0.6 = 0.0864
.... 이어서 계산해준다.

- Evaluation vs Decoding
- Forward Algorithm for Evaluation - 가능한 모든 경우의 확률 합 / Observable state의 확률을 구하는 것이 목표
- Viterbi Algorithm for Evaluation - 가능한 모든 경우의 최대 확률 선택 / 가장 그럴싸한 상태를 찾는 것

728x90
'인공지능' 카테고리의 다른 글
| 인공지능(7) - K-Means Clustering (0) | 2025.03.10 |
|---|---|
| 인공지능(6) - K-Nearest Neighbor (0) | 2025.03.10 |
| 인공지능(4) - Minimax (0) | 2025.02.11 |
| 인공지능(3) - Fuzzy Logic (0) | 2025.02.10 |
| 인공지능(2) - Bayesian Inference (0) | 2025.02.06 |
