- 의사결정트리 (Decision Tree)란?
- 기계 학습에서 사용되는 지도 학습 알고리즘 중 하나로 데이터의 특징과 레이블간의 관계를 트리 구조로 표현하는 모델
- 의사결정트리 과정은 스무고개와 비슷한 방식으로 동작

- 의사결정트리의 목적
- 데이터의 특징과 레이블 간의 관계를 학습하고 이를 기반으로 예측 및 분류를 수행하는 것
- 예측 및 분류
- 주어진 입력 값에 대해 예측 값을 생성하고 분류를 수행
- 특징의 중요도 파악
- 트리의 규칙은 if-else형태로 표현되며 특징들이 어떤 순서로 사용되고 어떤 특징이 가장 분류에 중요한 영향을 미치는지 알려줌
- 이를 통해 데이터 셋의 특징을 이해하고 문제에 대한 통찰을 얻는데 도움을 줌
- 과적합 방지
- 가지치기 기법을 사용하여 불필요한 가지를 제거하여 과적합 방지에 활용됨
- Decision Tree 기본 예시
| 날씨 | 온도 | 습도 | 바람 | 운동 |
| 해 | 더움 | 낮음 | T | Yes |
| 해 | 더움 | 보통 | F | Yes |
| 흐림 | 더움 | 높음 | T | No |
| 비 | 시원 | 높음 | T | No |
| 흐림 | 적당 | 보통 | T | Yes |
| ... | ... | ... | ... | ... |
기상조건에 따라 운동을 갈지 말지 결정하는 모델 만들어보자.

위의 예시에서 문제점은 무엇일까? 어떤 feature를 먼저 사용하냐에 따라 여러가지 Decision Tree를 만들 수 있다.
- Decision Tree가 궁극적으로 하려는 것
- 여러 Decision Tree 중 어떤 모델이 좋은지 결정하는 것
- -> 변별력이 좋은 질문을 먼저 던지는 것이다.
- Decision Tree 동작 순서
- 전체 데이터
- 각 분할 후 엔트로피 계산
- 정보이득 계산
- 정보이득이 가장 큰 feature 선택
- 선택된 feature 기반 분기(데이터 정렬)
: 로그의 기본 의미
- 로그(Log)의 정의
- 어떤 수를 몇 번 곱해야 목표 수가 되는가를 묻는 연산
- Log₂
- 정보를 세는 기초 단위 / 어떤 정보를 처리할 때 몇 비트가 필요한가를 묻는 연산
| 수식 | 해석 |
| log₂8 | 2³ = 8 8을 표현할 땐 2³자리만큼 비트가 필요(=1000) |
: 정보량 (Information)
- 정보량의 정의
- 어떤 사건이 발생했을 때 그 사건이 주는 '놀라움' 또는 '정보의 양'을 수치로 표현한 것
Log₂ + 확률
- 수학적 정의
I(x) = -log₂P(x)
- P(x) : 사건 x가 발생할 확률
- I(x) : 사건 x가 발생했을 때 그 사건이 주는 정보의 양
- 특징
- 확률이 낮은 사건일 수록 더 많은 정보가 필요
: 엔트로피 (Entropy)
- 엔트로피의 정의
- 어떤 확률 분포의 평균 정보량 또는 무작위성(불확실성)의 정도를 나타냄
- 예측이 얼마나 어려운가를 수치로 표현한 값임
- 수학적 정의
H(x) = Ε[I(x)] = -ΣP(xᵢ)log₂P(xᵢ)
- P(xᵢ) : 사건 xᵢ가 발생할 확률
- H(x) : 확률변수 x의 엔트로피
- 특징
- 확률이 고르게 분포될 수록 -> 엔트로피 높음 (불확실성이 큼)
- 확률이 한쪽으로 치우침 -> 엔트로피 낮음 (예측이 쉬움)
: 불순도 (impurity)
-불순도란?
- 불순물이 포함된 정도, 데이터의 혼잡도를 나타내는 지표
- 특정 지표를 기준으로 데이터 셋을 나누었을 때 데이터의 불순 정도가 줄어 들수록 좋은 질문이다.
- 의사결정나무와 불순도
- 의사결정나무는 질문을 통해 데이터의 불순도를 낮추는 방향으로 분기하는 모델

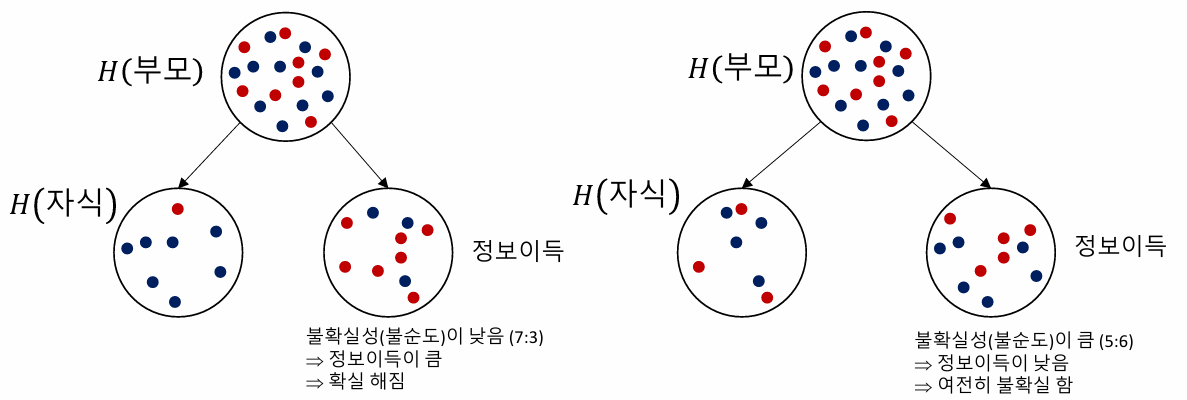
: 정보이득 (Information Gain)
- 정보이득 정의
- 의사결정나무에서 사용하는 용어로 어떤 속성을 기준으로 데이터를 분할할 때 얼마나 불확실성이 줄어드는지 수치로 나타내는 값
- 즉, 분할을 통해 얼마만큼 정보를 얻었는가를 계산하는 것
- 수학적 정의
Information Gain = H(부모) - H(자식)
- Decision Tree 예제
1. 전체 데이터
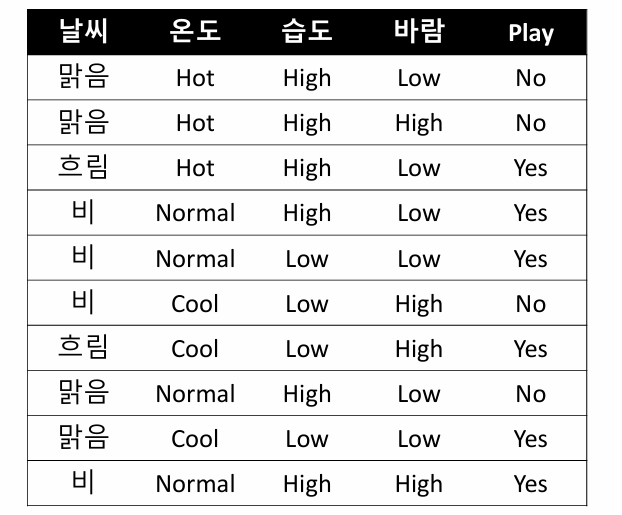
2. 각 분할에 대한 엔트로피 계산

| Play | ||||
| Y | N | Total | ||
| 날씨 | 맑음 | 1 | 3 | 4 |
| 흐림 | 2 | 0 | 2 | |
| 비 | 3 | 1 | 4 | |
H(날씨) = P(맑음)H(1,3) + P(흐림)H(2,0) + P(비)H(3,1)

| Play | ||||
| Y | N | Total | ||
| 온도 | Hot | 1 | 2 | 3 |
| Normal | 3 | 1 | 4 | |
| Cool | 2 | 1 | 3 | |
H(온도) = P(Hot)H(1,2) + P(Normal)H(3,1) + P(Cool)H(2,1)
=

= 0.892
| Play | ||||
| Y | N | Total | ||
| 습도 | High | 3 | 3 | 6 |
| Low | 3 | 1 | 4 | |
H(습도) = P(High)H(3,3) + P(Low)H(3,1)
=

= 0.924
| Play | ||||
| Y | N | Total | ||
| 바람 | High | 4 | 2 | 6 |
| Low | 2 | 2 | 4 | |
H(바람) = P(High)H(4,2) + P(Low)H(2,2)
=

= 0.951
3. 정보이득 계산
3.1 H(부모)에 대한 엔트로피 계산
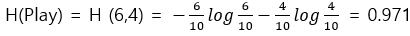
3.2 정보이득 계산
| 속성 | 엔트로피 | 정보이득 |
| 날씨 | 0.649 | 0.971-0.649 = 0.322 |
| 온도 | 0.892 | 0.971-0.892 = 0.079 |
| 습도 | 0.924 | 0.971-0.924 = 0.047 |
| 바람 | 0.951 | 0.971-0.951 = 0.020 |
4. 정보이득이 가장 큰 Feature인 날씨를 선택한다.

5. 선택된 Feature에 따라 분기 후 알고리즘 반복
| 날씨 | 온도 | 습도 | 바람 | Play |
| 맑음 | Hot | High | Low | No |
| 맑음 | Hot | High | High | No |
| 맑음 | Normal | High | Low | No |
| 맑음 | Cool | Low | Low | Yes |
앞선 단계처럼 엔트로피를 계산하면 날씨-맑음 에선 습도가 정보이득이 가장 크다.

...
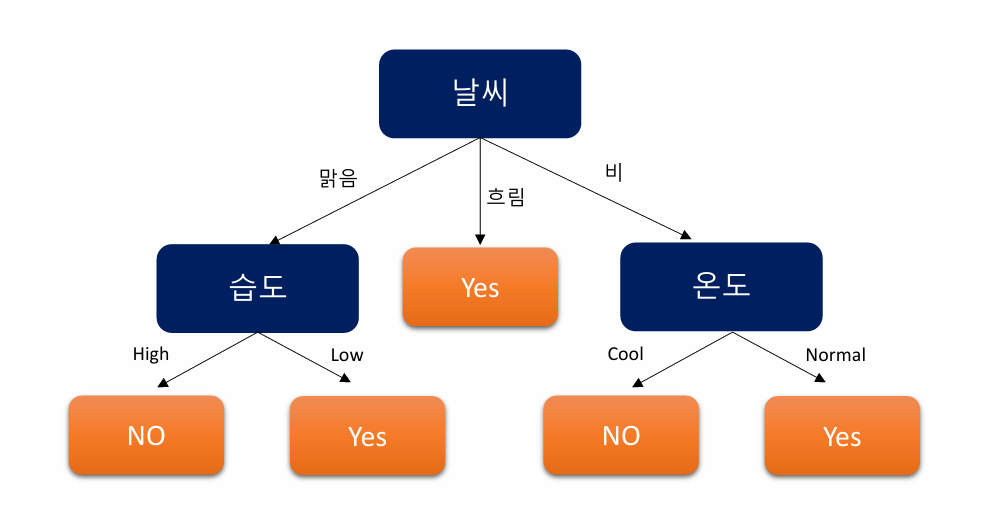
- 최종 결과
'빅데이터분석' 카테고리의 다른 글
| 빅데이터분석(4) - Feature Selection (0) | 2025.03.27 |
|---|---|
| 빅데이터분석(3) - T-SNE (0) | 2025.03.24 |
| 빅데이터분석(2) - PCA (0) | 2025.03.20 |
| 빅데이터 분석(1) - Data cleaning (0) | 2025.03.17 |
