728x90
- 저번 글에서 학습했던 주성분 분석(PCA)는 선형 분석 방식으로 값을 투영하기 때문에 군집화 되어 있거나 비선형 데이터에 대해서 올바른 동작이 어렵다는 한계가 있다. 이는 T-SNE로 해결가능하다.
T- distribution Stochastic Neighbor Embedding
- T-SNE란?
- 높은 차원의 복잡한 데이터를 저차원(2 또는 3차원)으로 차원 축소하는 방법
- 비선형 데이터에 대해서도 잘 동작하는 장점
- 오직 데이터의 시각화가 목표
- 핵심 아이디어
- 고차원에서 특정 데이터와 가까운 데이터는 저차원에서도 가까울 것이며, 멀리 떨어진 데이터는 저차원에서도 멀리 떨어져 있을 것이다.
- 가깝다/멀다 -> 이웃하다 -> Neighbor embedding
- 어떻게 판단? -> 확률적으로 Stochastic
- 어떤 확률 분포가 기준이 되나? -> T분포

T-SNE 동작 아이디어

1) 고차원 데이터에서 유사한 점 찾기 2) 저차원 공간에서 유사한 점 배치하기 3) 두 확률 분포(P, Q) 차이 줄이기 4) 최적화가 완료되면 데이터 구조를 시각화
- 1. Stochastic Neighbor Embedding
- Probability
- 특정 데이터 포인트 xᵢ가 주어졌을 때, 다른 데이터 포인트 xⱼ를 선택할 확률을 가우시안 분포를 이용해 계산

이때 σᵢ는 특정 데이터 포인트 xᵢ의 퍼플렉시티(Perplexity)를 조정하기 위해 설정되는 표준편차
- Perplexity
- 하나의 데이터 포인트가 평균적으로 몇 개의 이웃을 갖도록 할 것인가를 결정하는 값
- 가까운 이웃을 고를 때 어느 정도의 범위를 이웃이라 할지 정할 수 있으면 좋을듯? => perplexity (희망하는 복잡도)
- 하나의 데이터 포인트가 평균적으로 몇 개의 이웃을 갖도록 할 것인가를 결정하는 값

- 여기서 H(Pᵢ)는 샤논 엔트로피를 의미

- Perplexity와 표준편차 σᵢ 조정
- 초기값 설정
- σᵢ의 초기값 설정 (보통 1부터 시작)
- Perplexity 값을 설정한 후, 조건부 확률 Pⱼ|ᵢ의 엔트로피 H(Pᵢ)가 Perplexity와 맞아야 함
- 조건부 확률 Pⱼ|ᵢ 계산
- 현재 σᵢ 값으로 Pⱼ|ᵢ 확률 계산
- 아래 확률을 이용해 엔트로피 H(Pᵢ)를 계산
- 초기값 설정

3. 이진 탐색을 통한 σᵢ 조정
- 만약 H(Pᵢ) > log₂(Perplexity) 이면 σᵢ 를 줄임 (데이터를 더 집중 시킴)
- 만약 H(Pᵢ) < log₂(Perplexity) 이면 σᵢ 를 늘림 (데이터를 더 넓게 퍼뜨림)
- 이진 탐색을 반복하여 H(Pᵢ)가 log₂(Perplexity)에 가까워질 때까지 σᵢ 조정
- SNE의 목표
- 고차원에서의 데이터 분포와 저차원에서의 데이터 분포를 같게 만드는 것
- 분포를 같게 하는 방법? : Gradient Descent 기반 학습

- 2. T-distributed Stochastic Neighbor Embedding
- SNE의 문제점
- KL divergence의 비대칭 문제
- 가우시안 확률분포를 가정하여 발생하는 문제
- 이 두가지 문제를 해결한 것이 T-SNE이다.
- 고차원에서 유사도가 작은 값들이 많기 때문에 가우시안 분포를 사용하면 정보가 손실될 가능성이 높음
- T-분포는 꼬리가 두꺼워 저차원 공간에서 작은 거리 차이를 더 잘 반영할 수 있음

- KL divergence의 비대칭 문제 및 해결 방법
- KL divergence는 대칭적이지 않아서 다음과 같은 문제가 발생할 수 있음
- p가 높고 q가 낮을 때에는 cost가 높지만 p 가 낮고 q가 높을 때에는 cost 가 낮음
- 이 문제를 해결하기 위해 (대칭적으로 만들기 위해) 목적함수를 다음과 같이 재설정
- KL divergence는 대칭적이지 않아서 다음과 같은 문제가 발생할 수 있음
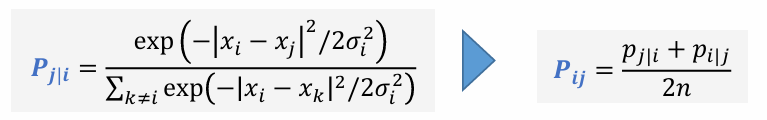
- TSNE의 주요 파라메터 (Python)
| NAME | Description |
| N_components | 기본값 : 2 차원 축소 결과 임베딩 되는 차원 |
| Perplexity | 기본값 : 30 Nearest neighbor의 범위를 설정하는 값 일반적으로 큰 데이터 셋은 큰 perplexity값을 요구 좋은 결과를 얻기 위해선 이 값을 5~50으로 변경하면서 실행 |
| Learning_rate | 기본값 : 200 학습할 때 사용되는 learning rate |
| N_iter | 기본값 : 1000 학습 횟수 |
| N_iter_without_progress | 기본값 : 300 조기 종료 옵션 성능 개선없이 학습이 n번 지속될 경우 조기 종료 |
- Perplexity 값에 따라 성능이 달라질 수 있다.

728x90
'빅데이터분석' 카테고리의 다른 글
| 빅데이터분석(5) - Decision Tree (0) | 2025.03.31 |
|---|---|
| 빅데이터분석(4) - Feature Selection (0) | 2025.03.27 |
| 빅데이터분석(2) - PCA (0) | 2025.03.20 |
| 빅데이터 분석(1) - Data cleaning (0) | 2025.03.17 |
