728x90
- Feature Selection (특성 선택)이란?
- 데이터의 특성(feature)중에서 가장 중요하게 생각되는 변수를 선택하는 것
- 학습 모델 훈련에 가장 유용한 특성을 선택하는 것이 목표
- 다시 말해 모델의 정확도를 향상시키기 위해 데이터 중에서 가장 좋은 성능을 보여줄 수 있는 데이터의 부분집합(subset)을 찾아내는 것
- Feature Selection의 이점
- 차원의 저주를 높임
- 모델의 성능을 높임
- 과적합 방지
- 계산효율이 좋아짐
- 데이터 분석에서 중요하지 않은 특성 제거

- Filter Method
- Filter Method : 데이터 셋에서 각 feature들의 통계적인 특성을 이용하여 feature들의 중요도를 평가하고, 이를 기반으로 feature를 선택하는 방법
- 대표적인 filter method
- 카이제곱검정 (Chi-squared Test)
- 상관계수 (Correlation coefficient)
- 상호정보량 (Mutual Information)
- filter method 원리
- 기준값(label)과 변수들 간의 관계성을 분석하여 관계가 깊은 변수를 중요한 변수로 간주하여 선택
- 카이제곱검정
- 범주형 데이터에서 사용되는 방법으로, 임의로 특정 feature를 선택하고 다른 feature간 독립성을 검정하여 feature의 중요도를 측정하는 방법
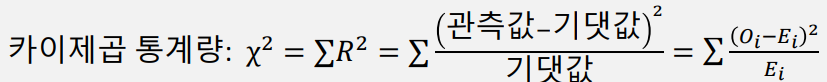
- 카이제곱 통계량을 구한 뒤 자유도에 따른 유의수준(0.05)을 비교하여 feature선택 여부를 결정
- 카이제곱검정 절차
- 가설 설정
- 유의수준 결정
- 기각 값 결정 (a값)
- 관찰도수에 대한 기대도수 계산
- 검정통계량 계산
- 귀무가설의 채택 또는 기각 여부 판정
- 카이제곱검정 예제

1. 변수 설정 및 교차 분할표 작성 (독립변수=진학여부, 종속변수=학력)
| 합격 | 실패 | 합계 | |
| 고졸 | 1 | 2 | 3 |
| 대졸 | 2 | 3 | 5 |
| 대학원졸 | 2 | 0 | 2 |
| 합계 | 5 | 5 | 10 |
2. 기대 도수 계산 -> (각 행의 합 * 각 열의 합) / 총합
| 합격 | 실패 | 합계 | |
| 고졸 | (3)(5)/10 = 1.5 | (3)(5)/10 = 1.5 | 3 |
| 대졸 | (5)(5)/10 = 2.5 | 2.5 | 5 |
| 대학원졸 | 1.0 | 1.0 | 2 |
| 합계 | 5 | 5 | 10 |
3. 카이제곱 통계량 계산 (위의 식 이용) / 1.67+1.67+0.1+0.1+1.0+1.0 = 2.53
| 합격 | 실패 | |
| 고졸 | 0.167 | 0.167 |
| 대졸 | 0.1 | 0.1 |
| 대학원졸 | 1.0 | 1.0 |
4. 가설검정
- 자유도가 2이고 유의수준 0.05일 때 카이제곱 임계값은 5.99
- 검정통계량은 2.53로 5.99보다 작아 귀무가설을 기각할 수 없음
- 따라서 부모의 학력과 자녀의 진학여부 사이에 유의미한 관계가 있다고 보기 어렵다.
- 상관계수 (Correlation)
- 상관계수 기반의 변수 선택
- 데이터간 상관계수를 구한 후 상관계수가 높을 경우 해당 변수를 선택
- 상관계수란
- 두 변수 사이에 관계의 정도를 나타내는 수치
- [-1,+1] 사이 값을 가지며 -1에 가까울 수록 음의 상관관계에 가깝고 +1에 가까울 수록 같은 데이터라 볼 수 있음. 0에 가까우면 둘 사이에 관계가 없음을 의미

- 장점
- 간단하고 직관적인 방법
- 변수 간 관계 파악이 쉬움
- 계산이 단순
- 단점
- 선형적 관계를 기반으로 하기 때문에 비선형적인 관계 분석 어려움
- 연관성을 보여주지만 인과관계를 설명하지 않음
- 누락된 데이터나 이상치에 민감하게 반응할 수 있음
- 상관계수 기반 변수 선택 예시
| x1 | x2 |
| 3 | 6 |
| 4 | 9 |
| 8 | 21 |
| 2 | 6 |
| 7 | 8 |
| 2 | 3 |
| 4 | 5 |
x1의 평균 = 4.28 ≈ 4
x2의 평균 = 8.28 ≈ 8
| X'1 | X'2 | X'1*X'2 | Σ |
| -1 | -2 | 2 | 68 |
| 0 | 1 | 0 | |
| 4 | 13 | 52 | |
| -2 | -2 | 4 | |
| 3 | 0 | 0 | |
| -2 | -5 | 10 | |
| 0 | -3 | 0 |
X'1과 X'2는 각각 x1,x2의 값에서 x1,x2의 평균을 뺀 값들
| A=(X'1)² | B=(X'2)² | ΣA * ΣB | √A*B |
| 1 | 4 | 34 * 212 = 7208 | 84.89 |
| 0 | 1 | ||
| 16 | 169 | ||
| 4 | 4 | ||
| 9 | 0 | ||
| 4 | 25 | ||
| 0 | 9 |

** x1 과 x2는 매우 유사하므로 x1만 변수로 채택
- 상호정보량(Mutual Information)
- 상호정보량이란
- 두 확률 변수 간 의존성을 나타내는 척도
- 두 변수간 의존성이 클 경우 해당 변수를 선택
- 상호정보량은 다음과 같이 정의

- 상호정보량을 이용한 변수 선택 과정
- 각 특성과 목표 변수 간의 상호정보량 계산
- 계산된 상호정보량을 기준으로 정렬
- 임계값을 기준으로 상위 순위의 특성을 선택
- 상호정보량 기반 변수선택 장단점
- 다른 변수 선택 방법보다 정확
- 비선형적 관계 변수도 분석 가능
- 비대칭성을 고려할 수 있으므로, 두 변수 간의 관계가 양방향인지 단방향인지 구분 가능
- 데이터가 희소한 (sparse) 경우에도 적용 가능
- 계산 비용이 크다는 단점 존재
- Wrapper Method
- Wrapper Method란
- 모델을 학습시키면서 변수를 선택하는 방법
- 특정 변수 조합에 대해 모델을 학습시켜 성능을 평가한 후 다음 라운드에서 특정 변수를 추가하거나 제거한 뒤 학습해가면서 최종 변수를 선택하는 방법
- 대표적인 방법
- 후진 소거법 (Recursive Feature Elimination, RFE)
- 장점
- 모델 성능을 향상시키는 최상의 변수 조합을 선택할 수 있음
- 과적합 방지를 위해 교차 검증과 같은 일반화 기술을 적용할 수 있음
- 단점
- 계산비용이 높으며 시간이 오래걸림
- 후진 소거법 (Recursive Feature Elimination, RFE)
- 가장 널리 사용하는 방법 중 하나
- 모든 변수를 다 포함시킨 후 학습을 진행하고 중요도가 낮은 변수를 하나씩 제거하는 방식
- 실행 과정
- 모든 특성을 포함하는 모델 선택
- 선택한 모델을 사용하여 특성의 중요도 계산
- 중요도가 가장 낮은 특성 제거
- 특성 제거 후 남은 특성으로 새로운 모델 학습
- 1~4과정 반복하며 미리 지정한 특성의 개수나 중요도에 따라 특성 선택
- 장단점
- 모델의 성능을 극대화하는 특성 집합을 찾아낼 수 있음
- 특성의 중요도를 판단할 수 있음
- 특성을 선택하는데 시간이 오래 걸린다는 것과 모델에 따라 결과가 달라질 수 있다는 것이 단점
728x90
'빅데이터분석' 카테고리의 다른 글
| 빅데이터분석(5) - Decision Tree (0) | 2025.03.31 |
|---|---|
| 빅데이터분석(3) - T-SNE (0) | 2025.03.24 |
| 빅데이터분석(2) - PCA (0) | 2025.03.20 |
| 빅데이터 분석(1) - Data cleaning (0) | 2025.03.17 |
